We will now find the quantum operator of the angular momentum in the Z direction L_z. These are illustrated in Figure 3.
3 4 Angular Momentum Of An Electron In A Hydrogen Atom Chemistry Libretexts
ANGULAR MOMENTUM IN SPHERICAL COORDINATES B3 Angular Momentum in Spherical Coordinates The orbital angular momentum operator Z can be expressed in spherical coordinates as.

Angular momentum z component. Operator and the difierence of operators is another operator we expect the components of angular momentum to be operators. Here v perp is the component of the particles velocity perpendicular to the axis of rotation. The z-component of angular momentum of an electron in an atomic orbit is government by the The z-component of angular momentum of an electron in an atomic orbit is government by the Books.
LRxP-ilirrxV-ilirrx arar-aersinealpea a or as 635 B23 B24 L -ili e - sie aalp. However all we are really doing is transforming between Cartesian and spherical coordinates as you will see. The 2nd part is to find the probability of L_z -2 hbar.
L z XP y YP x. The caseml corresponds to the maximum angular momentum component alongthez-axis. According to the postulates that wehave spelled out in previous lectures we need to associate to each observable a Hermiteanoperator.
L 1 l nonumber for a given value of l. After isnt this what the Uncertainty Principle is all about. One might visualize the particle in thexy-plane rotating about thez-axisOf course it cant be exactly in thexy-plane and its out of plane motion produces somecomponents of LxandLywhich average to 0 but have some spread around the averageThe uncertainty relation becomes.
The angular-momentum eigenfunctions are completely specified by j and m. Theres nothing special with this axis except that when used as the quantisation axis the. Spin projection m s 12 is referred to as spin up whereas m s 12 is called spin down.
Thats why physicists tell us that in quantum mechanics the angular momentum is never completely along the z-direction It is obvious that this actually challenges the idea of a very precise direction in quantum mechanics but then that shouldnt surprise us does it. For a quantum system the angular momentum is an observable we canmeasurethe angularmomentum of a particle in a given quantum state. We have already defined the operators Xˆand Pˆ associated respectively to theposition and the momentum of a particle.
The direction of the angular momentum is given by the right-hand rule. If the component of the net external torque on a system along a certain axis is zero the component of the angular momentum of the system along that axis cannot change no matter what changes take place within the system. In other words quantum mechanically L x YP z ZP y.
It is the z component of angular momentum. This conservation law holds not only within the frame of Newtons. I have tried using the operator form of L_z frachbari fracpartialpartial phi but that is not very helpful.
The z-component of the angular momentum ie projection of L onto the z-axis is also quantized with L_z m_l hbar nonumber with m_l -l 0-1 0. Angular momentum is the vector sum of the components. By convention we assume this axis to be the z axis.
We will show the direct proof for the z component as it is the most common of the three seen in literature. Angular momentum is a vector. S z is the z-component of spin angular momentum and m s is the spin projection quantum number.
The ground state has a degeneracy of two because the total angular momentum can have a z-axis projection of frac 12 hbar or -frac 12 hbar corresponding to m_J 12 or -12 resulting from the two electron spin states alpha and beta. It is more tedious work. The magnitude of the orbital angular momentum of the particle is L mrv perp mr 2 ω.
Magnitude and m is characteristic of the z component of the angular momentum. Using B24 along with B2 to BA we express the components ix Ly Lz within the con. The sum of operators is another operator so angular momentum is an operator.
This eigenvalue corresponds to the operator for Lz and Lz is the z component. Hence the functions can be represented by kets written as jj ml Section A54. We have not encountered.
For electrons s can only be 12 and m s can be either 12 or 12. L y ZP x XP z. These are the components.
In case of quantum mechanics of the 3 directions available one can choose any one of them to be the quantisation axis. The answer lies in the question itself. For this is realize I need to do the inner-product of the m -2 state with the original wavefunction but how do.
Traditionally ml is defined to be the z component of the angular momentum l and it is the eigenvalue the quantity we expect to see over and over again in units of ℏ of the wave function ψ.

Chm 2 S 1 A Introduction To Quantum

Quantum Numbers And Rules Physics

Chapter 7 The Hydrogen Atom Orbital Angular Momentum

Quantum Numbers And Rules Physics
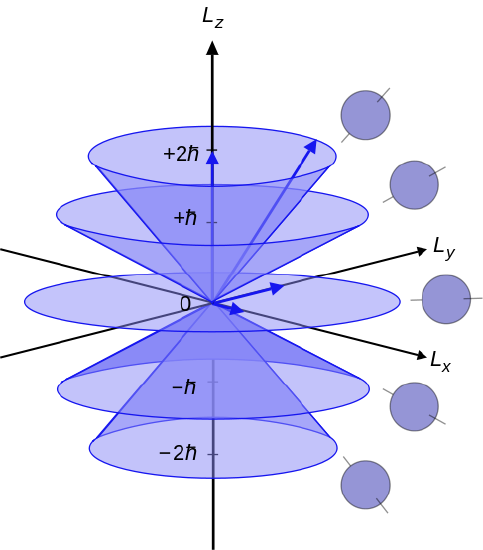
6 3 The Three Components Of Angular Momentum Cannot Be Measured Simultaneously With Arbitrary Precision Chemistry Libretexts
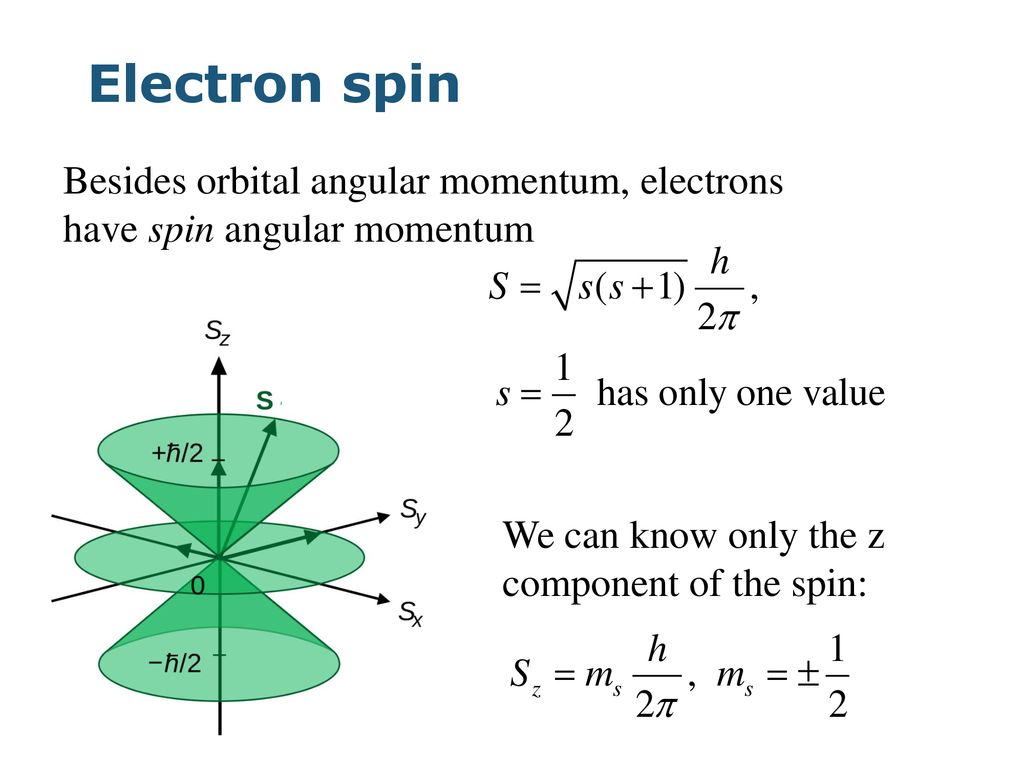
Hydrogen Atom Energy Levels Ppt Download

The Z Component Of Angular Momentum Of An Electron In An Atomic Orbit Is Government By The
For Two Electrons The Z Component Of The Total Chegg Com
Quantization Of Angular Momentum
Quantization Of Angular Momentum
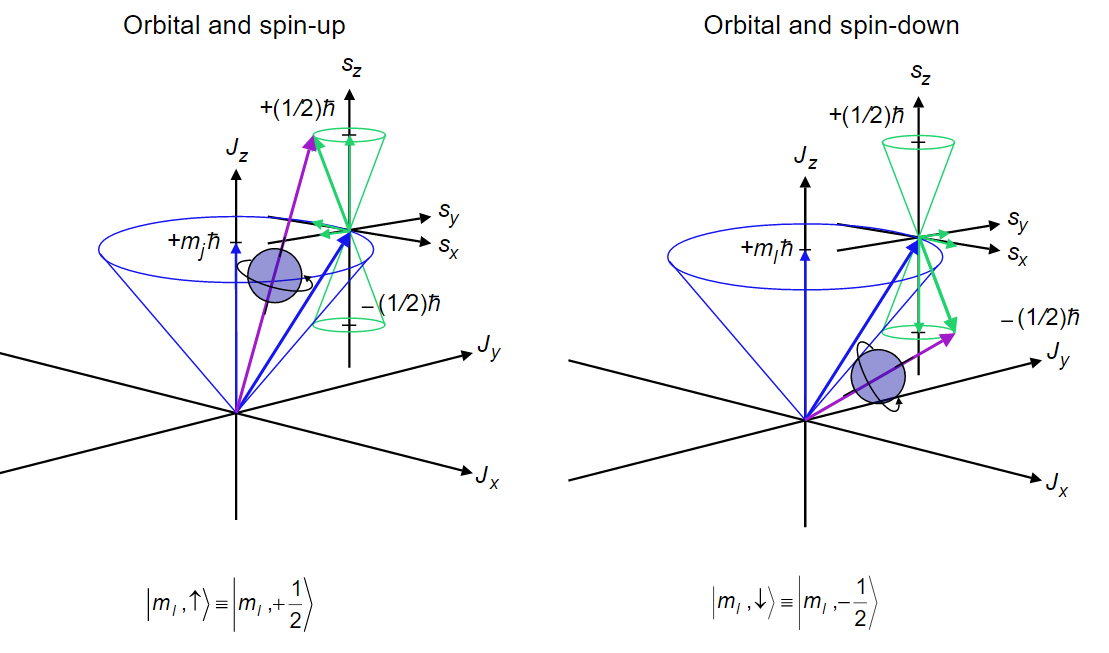
8 9 The Allowed Values Of J The Total Angular Momentum Quantum Number Chemistry Libretexts

Total Angular Momentum Ppt Download
Sample Question Electron Spin And Orbital Angular Momentum Qs Study
What Is Electron Spin Real Rotation




0 Comments